Quadrilaterals
Purpose of the article:
Hello Reader,
I see that you are looking to know about various types of quadrilaterals.
- Well, you have landed just at the right place.
In this article,
- You will get an idea about the quadrilateral and its various types.
You will also get to know about the properties of a few special kinds of quadrilaterals.
As you progress through this article, you will get the chance to test your learnings by attempting two quizzes.
- A.Quiz - 1: This is a pre-quiz. You can take this quiz to check your current knowledge of quadrilateral and its properties.
B.Quiz 2: This is a post-quiz that will check your understanding once you have read the article.
So, lets get straight into it.
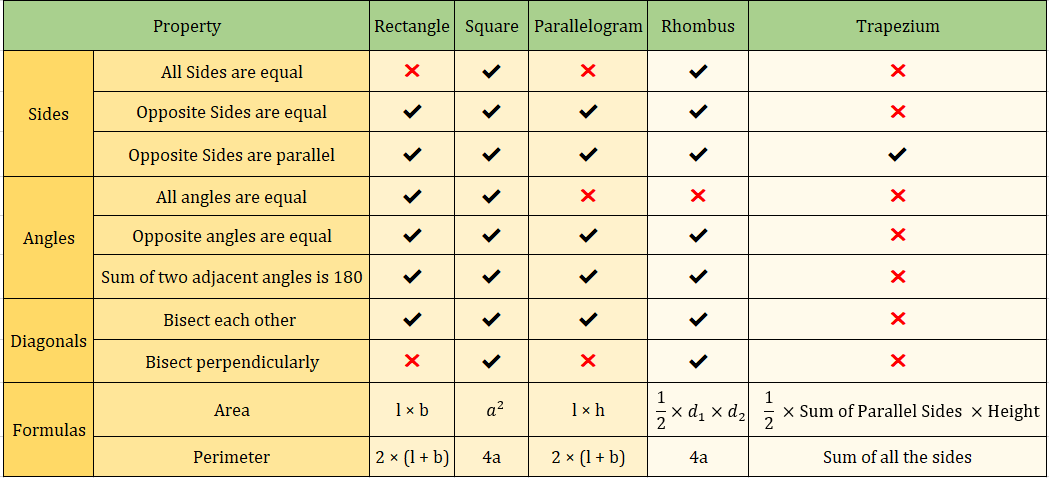
What is a quadrilateral?
A quadrilateral is a polygon that has 4 sides.
- So, any closed figure that has 4 sides is a quadrilateral.
And, all the angles of a quadrilateral sum up to 3600.
The diagram given below shows a quadrilateral ABCD and the sum of its internal angles.
Various kinds of quadrilateral
There are some special kinds of quadrilateral that we see in our textbooks/ exams.
These are:
- 1.Rectangle
2.Square
3.Rhombus
4.Parallelogram
5.Trapezium
Let us discuss each type in detail.
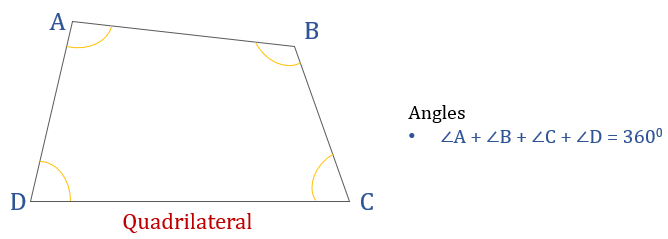
Rectangle
A rectangle is a quadrilateral:
- Each of the 4 angles are \(90^o\)
And, opposite sides of a rectangle are equal and parallel
Diagonals of a rectangle bisect each other
Formulas to remember
If the length of the rectangle is L and breadth is B then,
- 1.Area of a rectangle = Length Breadth or L B
2.Perimeter of rectangle = 2 (L + B)

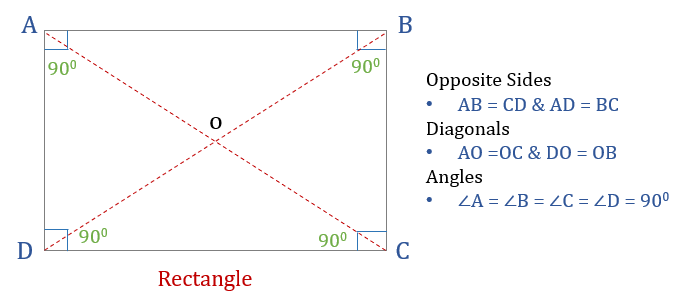
Square
A square is a quadrilateral:
- That has all the angles as \(90^o\)
All sides of a square are equal
- oAnd, opposite sides are parallel to each other
Diagonals bisect each other perpendicularly

Formulas to remember
If the side of a square is a then,
- 1.Area of the square = \(a a = a^2\)
2.Perimeter of the square = 2 (a + a) = 4a
Parallelogram
A parallelogram is a quadrilateral in which:
- Opposite angles are equal
Opposite sides are equal and parallel
Diagonals bisect each other
Sum of any two adjacent angles is \(180^o\)

Formulas to remember
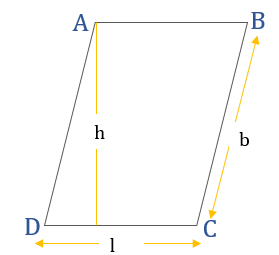
If the length of a parallelogram is l, breadth is b and height is h then:
- 1.Perimeter of parallelogram= 2 (l + b)
2.Area of the parallelogram = l h
Rhombus
A rhombus is a quadrilateral in which:
- Opposite angles are equal
All sides are equal
- oAnd, opposite sides are parallel to each other
Diagonals bisect each other perpendicularly
Sum of any two adjacent angles is \(180^o\)
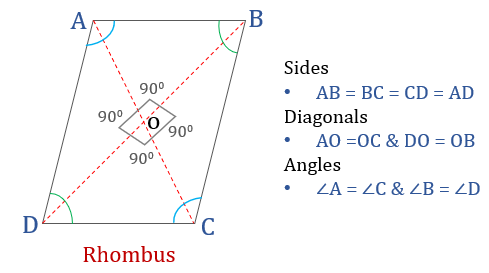

Formulas to remember
- If the side of a rhombus is a then,
- Perimeter of rhombus= 4a
If the length of two diagonals of the rhombus is d1 and d2 then:
- Area of the rhombus = \(\frac{1}{2} d_1 d_2\)
Trapezium
A trapezium is a quadrilateral in which:
- Only one pair of opposite sides are parallel to each other
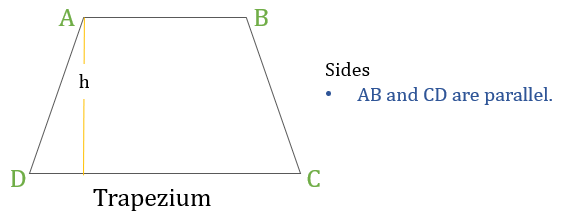
Formulas to remember
- If the height of a trapezium is h (as shown in the above diagram) then:
- Perimeter of the trapezium= Sum of lengths of all the sides = AB + BC + CD + DA
Area of the trapezium = \(\frac{1}{2}\) (Sum of lengths of parallel sides) h
= \(\frac{1}{2}\) (AB + CD) h
Summary of all the properties we learnt